[LSL] 位置と回転について ～クォータニオンと移動量～

前回からの続き、、、ではなくて、ちょっと閑話休題。といっても、今回の一連のお話しの中で、私が勝手に造語的に使っている「移動量」って何？の補足みたいなお話しです。

[LSL] 位置と回転について ～移動量という考え方～ のエントリーで、球体で考える空間と位置指定の概念を説明するのに、地球の話を持ってきて「移動量」の話をしていますが、この移動量っていうのが、やっぱりよくわかんない、、、と感じる方も多いと思います。

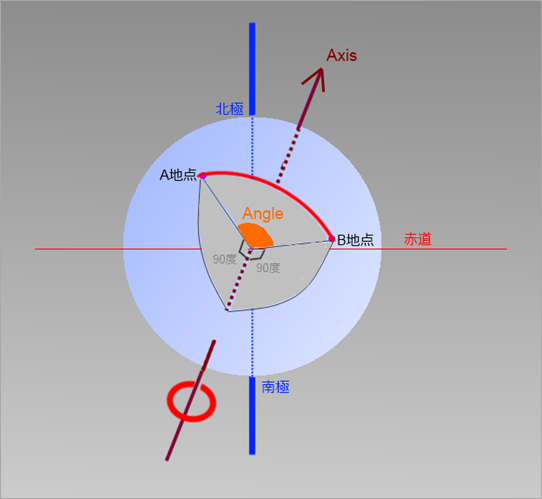
移動量（正直、これ私が勝手にそう呼んでいるので、一般的な用語ではないことをご了承ください。）はクォータニオンそのものなんですが、イメージとしては地球上のある地点から他の地点までの最短距離（大圏航路）で、ぐるっ！と地球をまわして、一度の回転でA地点からB地点にいって、回転させる軸の傾きも含めたもの、、、としつこく書いています。

ふ～ん、そうなんだ、と思ってくれるといいのですが、「ん～、わかんない」となると、実は先に進めないのも事実。それが2年前の私の状態ですから（笑
イメージ、イメージっていってもしょうがないので、もうちょっと具体的に説明してみたいと思います。ただし、なぜこれまで具体的に説明していないか、、、といえば、最終的には必要になる場合もありますが、最初のほうでは具体的に理解する必要があまりない（というか邪魔な？）知識だと思ったためです。あ、もちろん、ここでも行列計算、虚数といった数学的な話にはなりません。

前のエントリーでも「羽田空港とJFK空港を結ぶ大圏航路でグルッと回す」、それが移動量って言い方をしていますが、一気に回すための傾いた軸って存在しますよね。

クォータニオンからは、まず、その軸の方向を導き出すことができます。その関数が llRot2Axis なんです。そして軸を使ってまわした角度が llRot2Angle なんです。

( 絵心無いわ・・・わかってくれるといいけどｗ )

この軸の傾き（方向）と回る角度が移動量つまりクォータニオンを構成する要素なんですよね。
実際、Axis のベクターと、Angle の float からクォータニオンを計算する関数が llAxisAngle2Rot になるわけです。これでクォータニオン（移動量）を算出できるのです。

ネットや書籍でクォータニオンを調べると、そもそも LSL で使われる関数などでは説明されませんから、四元数で、実数部分と虚数部分にわかれ、、、、と説明されます。クォータニオンはローテーション型で <x, y, z ,s> の四元数にて LSL でも表現されますが、現実にその x, y, z, s の要素を直接いぢることは、最初の頃はほぼ皆無です。ちなみに2年前に私は ウィキペディアの四元数や、クォータニオンの説明を見てしまい、頭痛＆挫折しそうになりましたし、wiki.secondlife.com での llRot2Axis や llRot2Angle の説明では、それらの関数と同じ動きをする llAcos や llFabs, llSqrt, llVecNorm で四元数の要素をいじるユーザー関数を紹介しています。ですが、その特記事項を見ても何を言っているのかわからなかったわけです。

実際はウィキペディアにある内容をもとにクォータニオンは計算され、四元数の各要素となって表現されるのですが、それを理解するためには数学の勉強は必須で、ちょっと敷居が高かったのです。（私にとっては、、、ですが）

このクォータニオンと軸の傾きと回転量の関係がわかっていれば、他のところでも応用可能なような気がしませんか？

回す軸の方向はわかっていて、何度まわしたい、、、ってあるでしょう？おおよそローカル軸が「回す軸の方向」なので、あまり Axis と Angle の関係を理解せずにｚ軸で回すなら <0.0, 0.0, PI/2> とかにして、llEuler2Rot を使ってクォータニオン（移動量）にして、現在の Rotation に左からかけたりする、、、。でも、ローカルの軸、もしくはグローバルの軸じゃなくても、llAxisAngle2Rot で任意の軸で回すことができる、、、と考えると、ちょっとどこかで使えそうな気がしません？

クォータニオンについては、最初の回で紹介したように、また、何度もしつこくいっているように「球体で考える空間と位置指定」の概念をきちんと持つことで、行列計算や三角関数を深く知らなくても、LSL の関数だけでほとんどの操作は克服できると思っています。その上のステップに行くときに、そこで必要な知識を吸収すればいいわけですよね。

さて、次はオブジェクトに座っているアバタ―を動かす（それも複数のアバタ―）です。