[LSL] 位置と回転について ～ 移動量という考え方 ～

前回、位置を表すには2つの方法があって、そのうちのひとつに地球を例にとって球体における位置の指定についてご紹介しました。

今回はその球体における位置指定について具体的に見ていきたいと思います。

2. 移動量という考え方

前回では成田空港と JFK 空港の位置は「緯度」と「経度」で指定できることをご紹介しました。緯度、経度が何か、、、はここでは詳しく説明しませんが、数値データで表現されるこの緯度、経度、、、それぞれの数値が 0 のところってどこでしょう？そしてそれはどんな意味を持つのか考えてみます。

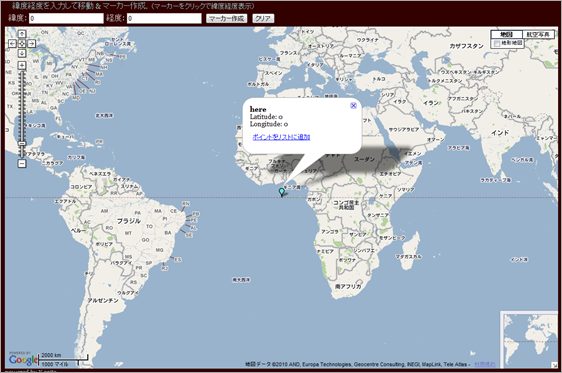
緯度０度（つまり赤道上）で、経度0度（つまり、イギリスのグリニッジ天文台を通過する子午線）が交わる地球上の位置は残念ながら海上です。アフリカのガーナの下、ギニア湾上にありました。（上の Google Map の 青いマーカーです）

この緯度・経度が 0 の地点から「ある移動量で動いた地点」をクォータニオンで表すことができるのです。クォータニオンはプリム/オブジェクトの「回転」で出てくる重要な要素ですが、前回ご紹介した大圏航路をつかってある地点、たとえば成田空港まで（球面上で）緯度0度、経度0度の地点から線を引く時、地球を「ぐるっ」と斜めになっている軸で回すと、それも1回の回転だけで青のマーカーを成田空港のある位置まで「移動させる」ことが想像できると思います。（今は軸が何度傾いて、、、とかは考えないようにします。地球を回すと成田空港も逃げちゃうよ、、という突っ込みはなしで＾＾； 気になる人は成田空港があった位置まで、、、とでも置き換えてください。）

緯度0度、経度0度から成田空港へは地球の裏側にいくので、成田とJFKで大圏航路を。。。。

この斜めの軸でぐるっと回し移動させる傾きも含めた「量」を移動量として理解します。そして、その移動量は回転なのでクォータニオンで表現できる、、、と覚えます。
そうすると、緯度0度、経度0度を基準点とした成田空港地点への移動量（クォータニオン）は、成田空港の位置そのものをあらわしていると言えます。

なんとなく、基準点さえ決まっていれば移動量を用いて場所の特定ができそうかな、、、と思ってもらえればいいのですが。

ただ、ここで疑問が湧きます。Seondlife のインワールドではグローバル座標による位置の指定は直観的で、<24.0, 120.0, 30.0> であれば <0.0, 0.0, 0.0> から X 軸のプラス方向に 24 m 進んで、Y 軸のプラス方向に 120m 進んで、Z 軸のプラス方向に 30m 上がれば、そこが指定されている位置だということはわかります。クォータニオンを使った場合、球体の中心は、、、えっと、SIM が 256m X 256m X 256m の立方体だから、その中心は 128m x 128m x 128m、、、あ、でも高さはもっと何千メートルもあるから、、、あれ、中心ってどこだろう？？？？と思います。私も最初のころは、これでつまづいていたんです。

クォータニオンを使った位置指定の重要なポイントは、上の疑問にあるように「球体の中心」をどこにもってくるか、、、なのですが、グローバル座標（リージョン座標）で考えるときは、そのものズバリ <0.0, 0.0, 0.0> を球の中心として考えるのです。
ん～、それですべての位置の表現ができるの？と思いますよね。クォータニオンによる位置の指定は直観的ではないので、もうすこし我慢してお付き合いください。

いきなり3次元だとつらいので、ちょっと高さは考えないで平面で移動量（クォータニオン）と位置についての関係を見てみたのが以下の絵です。

 

いわゆる同心円のお話しですが、ピンクの線を基準として青い線分だけ回ったとします。青い線の回転量は R1 の円上でも、R2 の円上でも、R3 の円上でも同じですよね。ただし、R に相当する半径の長さが違うので、A1, A2, A3 は違う位置をさしている、、、ということです。赤い線上の B1 ~ B3 についても同じことが言えます。回した角度（移動量）は同じでも、半径が違えば指し示す位置が違う、ということで、地球上の高さ/標高が違う同じ緯度・経度の位置の指定方法をイメージするとわかりやすいと思います。

移動量、つまりクォータニオンと、上述の半径 R、地球上でいえば標高の組み合わせで、空間上のすべての位置を指し示すことができる、ということになります。

グローバル座標では <0.0,0.0,0.0> を球体の中心として考えてもよさそう、、、と思いますが、上の例でのピンクの線の「基準」はいったいどれか、、、、基準とした中心が <0.0,0.0,0.0> 以外の場合は、、、など、もう少しこのあいまいそうな「基準」について考えることで、グローバル（絶対）位置とローカル（相対）位置の理解が深まるはずです。

次回は「基準」について考えてみます。