[LSL] 位置と回転について ～ ルートプリムと子プリムたち

前回ではリージョン座標軸で表現される位置をクォータニオンと球体の中心からの距離で置き換える方法をご紹介しました。空間の概念は X, Y, Z 軸による立方体だけでなく、球体での移動量と球体の中心からの距離で表現できる「球体で考える空間と位置指定」の概念の重要性がご理解いただけたかな、と思います。

ここまででオイラー角による回転について１度も触れていないのは面白いですよね。移動量という言葉を使って「角度」という言葉を使っていないわけです。

プリムをまわす、回転させるときに一番最初に覚えるのは軸を中心とした回転ですよね。わたしもそうでした。Z軸で９０度回転させる、なんてことをやるわけで、そのときラジアンによる角度表現が必要である、とか、llEuler2Rot という関数を知ったり、右ねじの法則、グローバル軸を基にした回転と、ローカル軸を基にした回転の違い、その方法を学ぶわけです。

もちろんオイラー角によるプリムの回転で事足りことも多いのですが、スクリプトでいろいろな操作をやろうとすると、はじめから角度がわかっていることって、、、少ないと思います。llGetPos や llGetRot、llGetObjectDetails, llGetLinkPrimitiveParams などで取れる数値は位置を表すベクター型であり、移動量をあらわすローテーション型のクォータニオンです。なので、位置ベクトルとクォータニオンを駆使して操作することになり、あらかじめ各軸の角度がわかっていれば使えるオイラー角による回転指定は、、、、実は、かぎられるような気がします。

前置きが長くなりましたが、今回は llSetLinkPrimitiveParams などで必須となるルートプリムと子プリムの関係、とくに位置（ローカルポジション）と向き/回転（ローカルローテーション）について考えてみたいと思います。

4. ルートプリムと子プリムたち

複数のプリムをリンクさせるとき、スクリプトを組み込む必要がなければ、あまりルートプリムがどれかを意識しないかもしれませんが、スクリプトをいれてなんらかの操作をしようとすると、ルートプリムがどれか、子プリムでもリンク番号は何番かが非常に重要になります。

基本的なリンク、リンクのさせかたについては wiki の記事や先輩諸氏のブログなどを参照してもらって、ルートプリムに入っているスクリプトから子プリムたちをどのように扱うかを見てみます。

ポイント１ リンクされた子プリムは「ルートだけ」とつながっている

ちょっといきなりハードルが高いかもしれませんが、プリムをリンクさせたとき、子プリムはルートプリムに対してリンクされている、ということを忘れるときがあります。１対１なら直感的ですが、子プリムの数が多くなり、造形的に階層構造のようなオブジェクトになったとき、見た目で土台になっているプリムを動かすと、それに「見た目」でのっているプリムが動きそうな気になるんですよね。

上の絵の緑色のルートプリムを動かせば、リンクされている子プリムたちはすべて追随するのですが、青いプリムを動かしても、見た目その上にある赤や黄色のプリムは動かない、、ということです。上のような単純なオブジェクトだと「当たり前じゃん」と思うでしょうが、造詣をしていって、見た目が子プリム同士関連しているように見えれば見えるほど、ルートだけにしかリンクしていないことを忘れます（笑

それが顕著にでるのが、プリムに座ったアバターを動かすときです。

どうしても座っているプリムを動かせば、座っている（＝リンクしている）アバターも動くような気がしてしまいますが、アバターはルートにリンクしているであって、見た目座っているプリムとはリンクしていないのです。

ポイント２ 子プリムの位置・回転はルートプリムが「基準」です

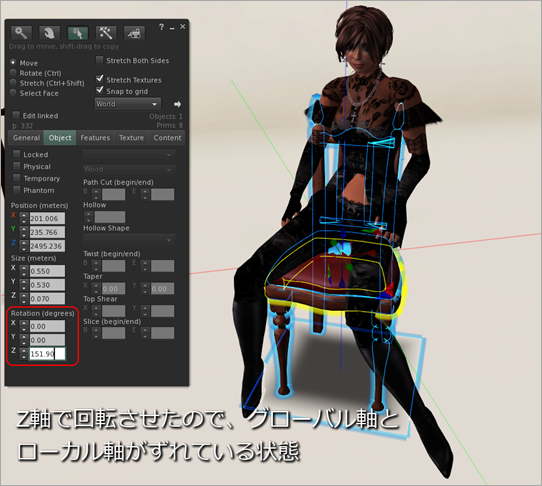
ですよね～、と思われるかもしれませんが、わたしも最初にはまった落とし穴は、ルートプリムのローカル座標軸（前後、左右、上下）がグローバル座標軸（東西、南北、天地）と重なっているのがおおよそ Rez した直後の初期値なので、グローバル座標軸を基準とした回転や位置指定を子プリムに対して行い、最初うまく動いている！と誤解してしまうことです。

うまく動いている状態だったのに、オブジェクトの向きを変えたら、予想もしない方向、位置に子プリムが動いた、、、となり、それが予想もつかない動きをするので悩んでしまう、、というものです。

ポイント3 ルートを基準とした位置の算出方法は球体で考える

正直、、、わたしは相当苦労しました。。。前に「位置と回転」について書いたブログが 2008 年のもの、、、当時はクォータニオンを理解しようとして行列計算や、関連しそうなネットの情報、書籍を読んでみて、興味深い内容が多かったものの、それぞれを理解したとはいえませんでした。

最近は wiki.secondlife.com のコンテンツも有志の方による日本語訳が充実してきているので、そこからある程度「こんなものかな」で理解してしまうほうがいいかもしれません。

ルートと子プリムの関係は、これまでご説明してきた「球体で考える空間と位置指定」の概念がわかっていれば比較的簡単に必要な数値の算出が可能になります。（なると思っています、、、）

まず、ルートから見た子プリムの相対位置です。
llGetLinkPrimitiveParams もしくは llGetObjectDetails で子プリムのグローバル座標を取得することができます。ルートプリムのグローバル座標もこの関数以外に llGetPos や llGetRootPosition で取得できるので、ルート、子プリムそれぞれのグローバル座標をもとに、ルートプリムからルートのローカル座標（前後、左右、上下）による子プリムまでの「軸上の移動距離」を算出することになります。ただし、この算出の場合も「球体で考える空間と位置指定」を使うことになります。

え？子プリムのグローバル座標からルートプリムのグローバル座標を引けばいいんじゃない？と思いたくなるのですが、その差分はグローバル座標軸における差（東西、南北、天地）であって、ルートプリムからのローカル座標軸（ルートプリムからの前後、左右、上下）での差分ではないのです。グローバル軸とローカル軸が重なっていれば問題ないですが、ずれた（ルートが回転した）瞬間から予期しない動きをしてしまいます。

ルートプリムから見た子プリムのローカル座標上の移動距離を算出する考え方と手順が以下になります。

a) 球体で考える空間と位置指定の概念を使ってルートプリムを球体の中心にもってくるイメージをしてみます

そのときのルートプリムの向きは llGetRot でとったそのままの傾きで、子プリムと一緒に動いてくるイメージです。球体の中心にきた時は、ルートプリムのローカル座標軸とグローバル座標軸はずれている感じです。そしてそのずれは移動量であり、ルートプリムのローテーションになります。

//ルートプリムのクォータニオン
rotation rootRot = llGetRot(); または llGetRootRotation();

b) 中心（ルート）から子プリムまでの直線距離とグローバル座標軸上の移動距離を算出します

グローバル座標軸における2つの位置ベクトル間の距離です。

vector rootPos  = llGetPos(); または llGetRootPosition();
integer linkNum = 2; //ルートは1、それ以降は2～ 
list pList  = llGetLinkPrimitiveParams(linkNum,[PRIM_POSITION]);
vector childPos = llList2Vector(pList,0); 
float dist = llVecDist(rootPos, childPos);

グローバル座標上の子プリムの位置とルートプリムの位置の差分。つまり、ルートプリムが中心のときにグローバル座標上の子プリムの位置ベクトルになります。

vector childVec = childPos-rootPos;

c) ルートプリムをぐるりと回転させて、ルートプリムのローカル座標軸とグローバル座標軸を一致させるイメージを持ってみます

この時の移動量は a) の rootRot だけ「戻る」感じですよね。
ただし、このとき「移動」するのは実は子プリムなんです。ルートプリムは中心にいるので一切「移動」しないわけです。
なので、動かす前の子プリムの移動量を算出します。これは子プリムの向きを表すローテーションではありません。球体で考える空間の話を思い出してください。球体の中心（＝ルートプリム）とX軸基準 <1.0, 0.0, 0.0> と自分のグローバル座標上の位置ベクトルから算出する移動量です。自分の位置ベクトルはグローバル座標上の XYZ であり、ルートプリムは球体の中心にきていますから、b) で算出した childVec になります。

rotation childRot = llRotBetween(<1.0,0.0,0.0>,childVec);

そして、ルートのローカル軸をグローバル軸にあわせるために、子プリムの移動量からルートの傾き分の移動量を引きます。（ルートプリムがぐるりとまわって元に戻る感じです。）ローテーションでの計算では除算します。ここがルートと子プリムの関係の最大のポイントです。

rotation q = childRot/rootRot;

これで移動量 q は、ルートのローカル軸、グローバル軸が重なった時点での球体上の子プリムの移動量となります。

d) ローカル座標の位置ベクトルを算出します

ローカル座標とグローバル座標は一致しているので、<1.0, 0.0, 0.0> と llRot2Fwd と使ったこれまでと同じ方法で算出します。

vector offset = llRot2Fwd(q)*dist;

この offset ベクターがルートプリムからの相対位置になります。
どうです？三角関数とか意識しなくても出せるような気がしませんか？
重要なのはイメージなんですよね。

と、、、ちょっと長くなったので、ルートプリムから見た子プリムの向きについては次回にします。